Zadaniem, jakie należy rozwiązać jest interpolacja funkcji, zadanej zbiorem 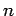 punktów:
punktów:
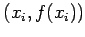 ,
,
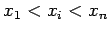 . Należy napisać program numeryczny, który na
podstawie podanego zbioru punktów oblicza poprzez interpolację przybliżone wartości
funkcji. Działanie programu przetestować należy dla funkcji
. Należy napisać program numeryczny, który na
podstawie podanego zbioru punktów oblicza poprzez interpolację przybliżone wartości
funkcji. Działanie programu przetestować należy dla funkcji
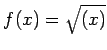 .
.
Rozwiązaniem podanego wyżej problemu jest zastosowanie wielomianu interpolacyjnego
stopnia co najwyżej 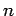 . W programie należy wykorzystać tzw. postać Lagrange'a:
. W programie należy wykorzystać tzw. postać Lagrange'a:
![$\displaystyle W_n(x) = \displaystyle\sum_{i=0}^{n}\left[f(x_i)\prod_{\overset{j=0}{i\neq j}}^{n} \frac{x-x_j}{x_i - x_j} \right]$](img6.png) |
(1) |
gdzie:
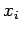 ,
, 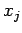 - wartości argumentów funkcji w punktach węzłowych,
- wartości argumentów funkcji w punktach węzłowych,
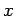 - argument, dla którego obliczana jest przybliżona wartość funkcji
- argument, dla którego obliczana jest przybliżona wartość funkcji 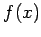 .
.
Interpolacją nazywamy wyznaczenie przybliżonej wartości funkcji 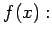
![$ [a,b]
\rightarrow \mathbb{R}$](img12.png) w dowolnym punkcie
w dowolnym punkcie
![$ x \in [a,b]$](img13.png) na podstawie znanych wartości
funkcji w ustalonych punktach
na podstawie znanych wartości
funkcji w ustalonych punktach 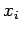 :
:
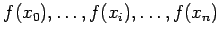 . Funkcja
interpolująca
. Funkcja
interpolująca 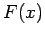 musi spełniać następującą własność:
musi spełniać następującą własność:
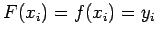 |
(2) |
Najczęściej stosowanym rozwiązaniem jest wykorzystanie jako funkcji interpolującej
wielomianu 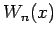 , którego stopień wynosi co najwyżej
, którego stopień wynosi co najwyżej 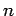 . Można udowodnić, że istnieje
dokładnie jeden wielomian interpolacyjny
. Można udowodnić, że istnieje
dokładnie jeden wielomian interpolacyjny 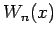 , który w punktach
, który w punktach
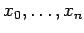 przyjmuje wartości
przyjmuje wartości
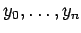 .
.
Wyprowadzenie równania (1) przeprowadza się poprzez konstruowanie tzw.
wielomianów pomocniczych 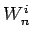 ,
,
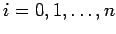 . Każdy z wielomianów pomocniczych
jest stopnia co najwyżej
. Każdy z wielomianów pomocniczych
jest stopnia co najwyżej 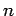 . Wielomiany te przyjmują wartość 0 w punktach
. Wielomiany te przyjmują wartość 0 w punktach 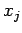 dla
dla 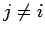 oraz 1 w punkcie
oraz 1 w punkcie 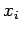 :
:
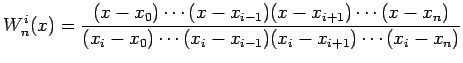 |
(3) |
Wygodnie jest zapisać równanie (3) w bardziej zwięzłej postaci:
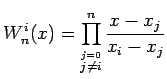 |
(4) |
Ze względu na podane wyżej własności, wielomian taki posiada następującą cechę:
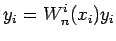 |
(5) |
Poprzez zsumowanie tak skonstruowanych wielomianów otrzymujemy również wielomian stopnia
co najwyżej 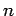 , dodatkowo spełniający warunki stawiane funkcji interpolującej:
, dodatkowo spełniający warunki stawiane funkcji interpolującej:
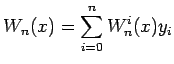 |
(6) |
Podstawiając do równania (6) równanie (4)
otrzymujemy:
![$\displaystyle W_n(x) = \displaystyle\sum_{i=0}^{n}\left[f(x_i)\prod_{\overset{j=0}{i\neq j}}^{n} \frac{x-x_j}{x_i - x_j} \right]$](img6.png) |
(7) |
Dla realizacji podanego powyżej schematu obliczeniowego (1) zastosować można
następujący algorytm:
 = 0.0; = 0.0; |
|
|
| dla i:= 1 do n wykonuj |
|
|
| rozpocznij |
|
|
 = 1.0; = 1.0; |
|
|
| dla j:= 1 do n wykonuj |
|
|
| rozpocznij |
|
|
| |
jezeli i 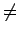 j wtedy j wtedy |
|
| |
|
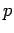 = = 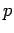 * ( * (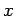 - - 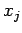 ) / ( ) / (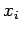 - - 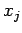 ); ); |
| zakoncz |
|
|
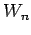 := := 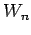 + + 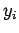 * * 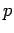 ; ; |
|
|
| zakoncz |
|
|
Przykład 1 Obliczenie interpolowanej wartości
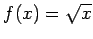
Przyjmijmy 3 punkty interpolacyjne:
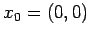
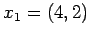
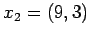
Dla 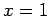 wartość interpolowana wynosi 6.00000000e-01. Otrzymany wynik daleki jest od
oczekiwanego. Dla poprawienia jakości przybliżenia zmniejszono odległość
pomiędzy punktami skrajnymi:
wartość interpolowana wynosi 6.00000000e-01. Otrzymany wynik daleki jest od
oczekiwanego. Dla poprawienia jakości przybliżenia zmniejszono odległość
pomiędzy punktami skrajnymi:
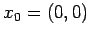
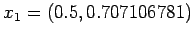
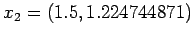
Wartość interpolowana dla 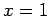 wynosi 1.11535507e+00.
wynosi 1.11535507e+00.
Przykład 2 Przykład zastosowania interpolacji
Rysunek 1 przedstawia interpolację funkcji danej równaniem
(8) za pomocą wielomianu stopnia czwartego.
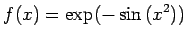 |
(8) |
Rysunek:
Wykres funkcji
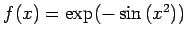
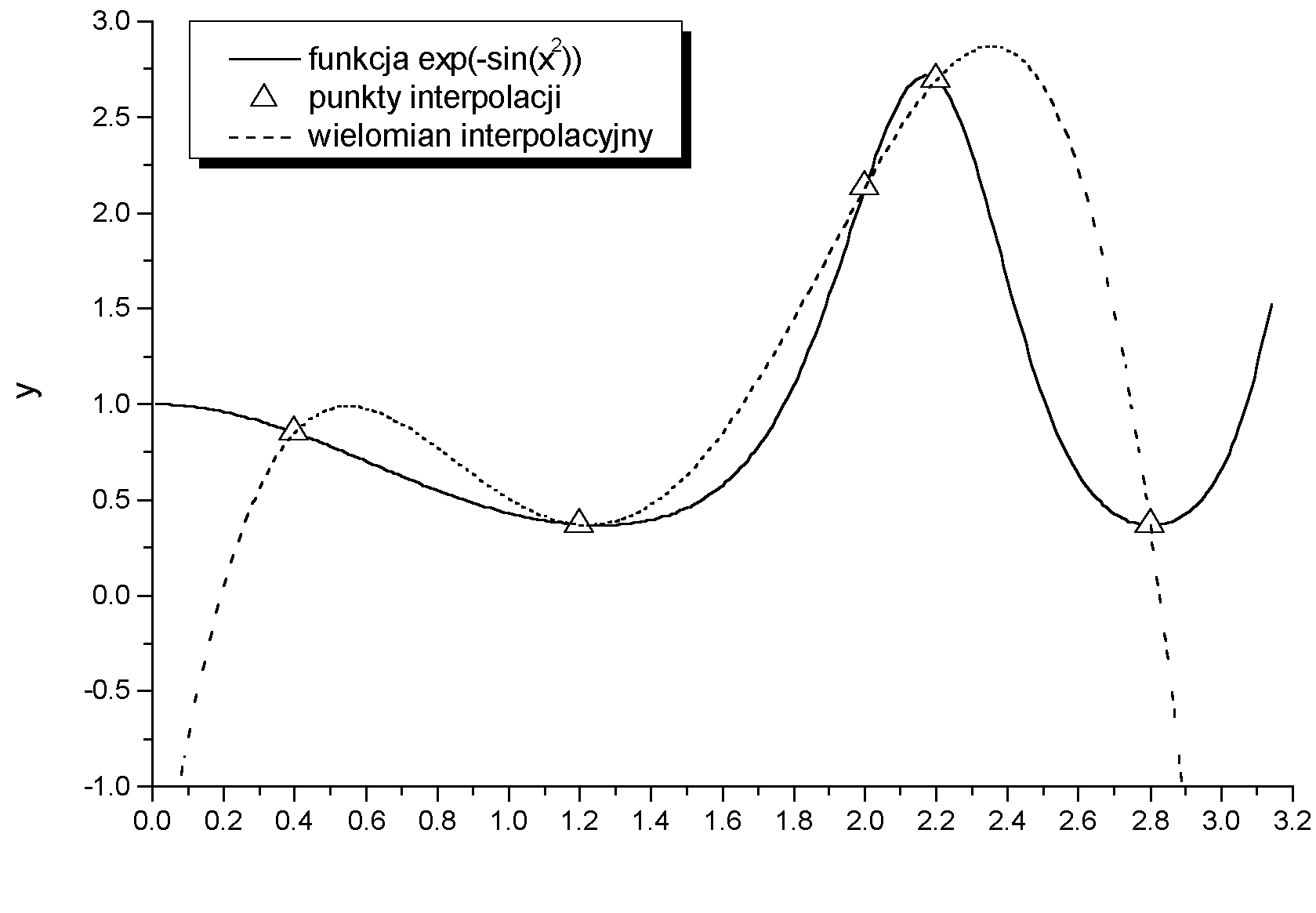 |
Jak można zauważyć, różnice występujące pomiędzy ,,oryginalnymi'' a interpolowanymi
wartościami są znaczące. Podstawowym błędem jest tutaj założenie, że za pomocą wielomianu
interpolacyjnego można obliczyć cały zakres zmienności funkcji. Tymczasem interpolację
stosuje się dla:
- niewielkich zakresów zmienności funkcji,
- niewielkich odległości pomiędzy punktami węzłowymi,
- lokalnie dostatecznie ,,gładkich'' funkcji.
Uwagi
- Jak zademonstrowano powyżej, interpolacja daje zadowalające wyniki (dla punktów
innych niż węzłowe) tylko wtedy, gdy odległości pomiędzy punktami węzłowymi są
stosunkowo niewielkie.
- W przypadku użycia do interpolacji wielomianów wysokiego stopnia (w praktyce
oznacza to stopień piąty i wyższe) kształt funkcji interpolującej pomiędzy punktami
węzłowymi może mieć charakter oscylacji. Jest to efekt silnie niepożądany.
- Z powodów przedstawionych w punktach 1 i
2 do opracowywania danych doświadczalnych stosuje się zazwyczaj
aproksymację (a nie interpolację).
- Interpolacja znajduje jednak bardzo duże zastosowanie w analizie różnego
rodzaju zagadnień teoretycznych z zakresu metod numerycznych. Wykorzystuje się ją
m.in. przy wyprowadzaniu wzorów na numeryczne całkowanie i różniczkowanie oraz przy
konstrukcji schematów rozwiązywania równań różniczkowych.
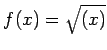 .
.
![]() ,
,
![]() . Każdy z wielomianów pomocniczych
jest stopnia co najwyżej
. Każdy z wielomianów pomocniczych
jest stopnia co najwyżej ![]() . Wielomiany te przyjmują wartość 0 w punktach
. Wielomiany te przyjmują wartość 0 w punktach ![]() dla
dla ![]() oraz 1 w punkcie
oraz 1 w punkcie ![]() :
:
![]()
![]()
![]()
![]() wartość interpolowana wynosi 6.00000000e-01. Otrzymany wynik daleki jest od
oczekiwanego. Dla poprawienia jakości przybliżenia zmniejszono odległość
pomiędzy punktami skrajnymi:
wartość interpolowana wynosi 6.00000000e-01. Otrzymany wynik daleki jest od
oczekiwanego. Dla poprawienia jakości przybliżenia zmniejszono odległość
pomiędzy punktami skrajnymi:
![]()
![]()
![]()
![]() wynosi 1.11535507e+00.
wynosi 1.11535507e+00.