![\begin{displaymath}\begin{array}{ccc} \displaystyle x = \sqrt[m]{a} && (a \in \m...
...{N}) \\ & \Updownarrow &\\ &\displaystyle x^m = a & \end{array}\end{displaymath}](img1.png) |
(1) |
| (11) | |||
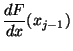 |
(12) | ||
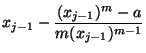 |
(13) |
| dla i:= 1 do nkrokow wykonuj | |
| rozpocznij | |
| zakoncz |
Zgodnie ze schematem obliczeniowym
danym równaniem (2) podstawiamy
![]() Równanie opisujące
Równanie opisujące ![]() -te
przybliżenie rozwiązania przyjmuje postać:
-te
przybliżenie rozwiązania przyjmuje postać:
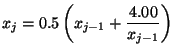
Poniżej zestawiono wyniki pierwszych 6 kroków metody.
| 4.0000000000e+000 |
|
2.5000000000e+000 | |
| 2.5000000000e+000 |
|
2.0500000000e+000 | |
| 2.0500000000e+000 |
|
2.0006097561e+000 | |
| 2.0006097561e+000 |
|
2.0000000929e+000 | |
| 2.0000000929e+000 |
|
2.0000000000e+000 | |
| 2.0000000000e+000 |
|
2.0000000000e+000 |
Przykład 2 Obliczanie pierwiastka kwadratowego z 2.0
Zgodnie ze schematem obliczeniowym
danym równaniem (2) podstawiamy
![]() Równanie opisujące
Równanie opisujące ![]() -te
przybliżenie rozwiązania przyjmuje postać:
-te
przybliżenie rozwiązania przyjmuje postać:
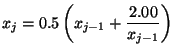
Poniżej zestawiono wyniki pierwszych 5 kroków metody.
| 2.0000000000e+000 |
|
1.5000000000e+000 | |
| 1.5000000000e+000 |
|
1.4166666667e+000 | |
| 1.4166666667e+000 |
|
1.4142156863e+000 | |
| 1.4142156863e+000 |
|
1.4142135624e+000 | |
| 1.4142135624e+000 |
|
1.4142135624e+000 |
Przykład
3 Obliczanie pierwiastka stopnia 7 z 3 (
![]() )
)
Poniżej zestawiono wyniki pierwszych 11 kroków metody.
| 3.0000000000e+000 |
|
2.5720164609e+000 | |
| 2.5720164609e+000 |
|
2.2060659436e+000 | |
| 2.2060659436e+000 |
|
1.8946316907e+000 | |
| 1.8946316907e+000 |
|
1.6332356394e+000 | |
| 1.6332356394e+000 |
|
1.4224965841e+000 | |
| 1.4224965841e+000 |
|
1.2710096113e+000 | |
| 1.2710096113e+000 |
|
1.1910921519e+000 | |
| 1.1910921519e+000 |
|
1.1710258809e+000 | |
| 1.1710258809e+000 |
|
1.1699338801e+000 | |
| 1.1699338801e+000 |
|
1.1699308128e+000 | |
| 1.1699308128e+000 |
|
1.1699308128e+000 |