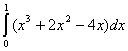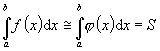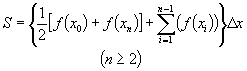Całkowanie numeryczne

1. Cel ćwiczenia

Celem ćwiczenia jest napisanie programu obliczającego całkę funkcji f(x) w przedziale [a,b] przy zastosowaniu następujących wzorów całkowania numerycznego:

1. wzoru trapezów
2. wzoru parabol
3. złożonego wzoru trapezów

Za pomocą programu należy wykonać obliczenia dla dwóch funkcji (a) i (b):

a)

dla wzoru trapezów, wzoru parabol oraz dla złożonego wzoru trapezów (liczba przedziałów częściowych: 10).

b)

dla wzoru trapezów, wzoru parabol oraz dla złożonego wzoru trapezów (liczba przedziałów częściowych: 10).

2. Wstęp teoretyczny

Analityczne obliczenie całki oznaczonej funkcji f(x) poprzez wyznaczenie funkcji pierwotnej może być bardzo trudne lub nawet niemożliwe, dlatego konieczne jest stosowanie metod przybliżonych. W przypadku, gdy przedział całkowania jest skończony funkcja podcałkowa f(x) zastępowana jest funkcją interpolującą j(x), którą można łatwo całkować. Czyli dokonujemy następującego przybliżenia:

2.1. Wzór trapezów.

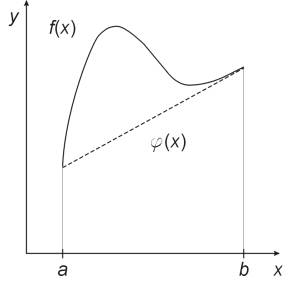
Metoda trapezów polega na tym, że funkcję podcałkową f(x) zastępujemy przez funkcję liniową: j(x) = ax+b przy czym spełnione są warunki: f(a) = j(a) oraz f(b) = j(b). Po przeprowadzeniu całkowania dla j(x) otrzymujemy następujący wzór:

wzór trapezów

2.2. Wzór parabol.

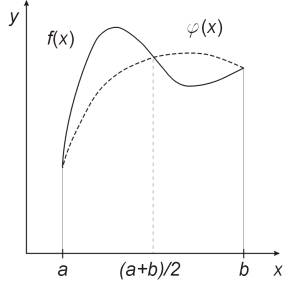
Metoda Simpsona (parabol) polega na tym, że funkcję podcałkową f(x) zastępujemy przez funkcję kwadratową: j(x) = ax²+bx+c przy czym spełnione są warunki: f(a) = j(a), f((a+b)/2) = j((a+b)/2) oraz f(b) = j(b). Po przeprowadzeniu całkowania dla j(x) otrzymujemy następujący wzór::

wzór parabol

2.3. Złożony wzór trapezów.

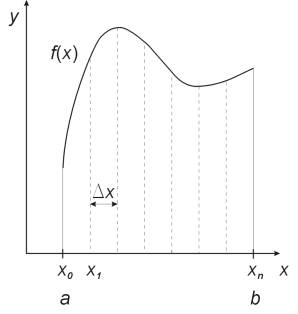
Przedział całkowania [a,b] dzielony jest na n przedziałów częściowych - wszystkie o tej samej długości Dx=(b-a)/n. Kolejne odcięte punktów podziału oznaczone zostają przez x₀, x₁,......, x_n, (x₀ = a, x_n = b), natomiast odpowiadające im rzędne przez y_i=f(x_i), (i=0,...,n). Przybliżoną wartość całki otrzymujemy po zastosowaniu prostego wzoru trapezów w każdym przedziale częściowym.

złożony wzór trapezów

3. Wyniki

Wynikiem działania programu powinny być następujące wartości:

wzór trapezów	-0,50000	1,20000
wzór parabol	-1,08333	0,84445
złożony wzór trapezów	-1,07750	0,81102
obliczenia analityczne	-1,08333	0,80472