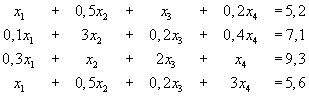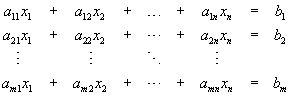
lub w postaci macierzowej
A x = b
Przekształcić należy do postaci
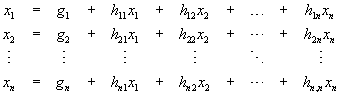
lub w notacji macierzowej
x = g + H x
gdzie:
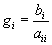
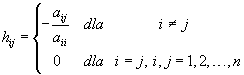
Metody iteracyjne (przybliżone) służą obliczaniu przybliżonych wartości pierwiastków układu równań liniowych za pomocą kolejnych aproksymacji. W tym celu należy przyjąć pewien dowolny wektor x(0) jako rozwiązanie początkowe i według określonego schematu tworzyć kolejno ciąg wektorów x(1), x(2),..., x(n),... tak, aby wektor x(n+1) lepiej przybliżał rozwiązanie dokładne od wektora x(n). Najprostszą metodą iteracyjnego rozwiązywania układu równań liniowych jest metoda Jacobiego
Celem ćwiczenia jest wykonanie programu, rozwiązującego liniowy układ równań o czterech niewiadomych, metodą Jacobiego lub Gaussa - Seidela. Do weryfikacji poprawności obliczeń wykorzystane mogą zostać podane przykłady.
W metodzie tej układ równań liniowych
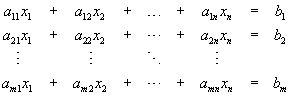
lub w postaci macierzowej
A x = b
Przekształcić należy do postaci
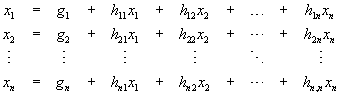
lub w notacji macierzowej
x = g + H x
gdzie:
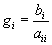
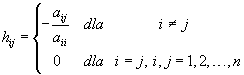
Na tym etapie należy sprawdzić zbieżność metody iteracji prostej dla danego zestawu parametrów. Warunkiem wystarczającym uzyskania zbieżności jest aby dowolna z norm macierzy H była mniejsza od jedności. Jako najprostsze można wykorzystać warunki
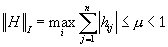
co oznacza, że największa z sum wierszy macierzy H jest mniejsza od jedności,lub
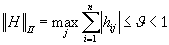
co oznacza, że największa z sum kolumn macierzy H jest mniejsza od jedności.
Kolejnym etapem jest iteracyjne wyznaczanie kolejnych przybliżeń wektora x. Jako wektor początkowy x(0) przyjmuje się zwykle wektor wartości zerowych lub wyrazów wolnych , tj. x(0) = g. Kolejne przybliżenia wyznacza się wg reguły
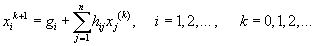
lub w postaci macierzowej
x(k+1) = g + H x(k), k = 0, 1, 2, ...
Metoda ta różni się od metody Jacobiego jedynie innym sposobem wyznaczania wektora x(k). Element xk1 wyznacza się tak samo, jak w metodzie Jacobiego, pozostałe zaś elementy wektora x(k)oblicza się korzystając zarówno z wartości wektora x(k-1), jak i z wyznaczonych już elemtów wektora x(k).
Wektor x(k) wyznacza się w oparciu o wyrażenie
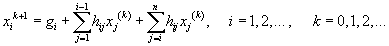
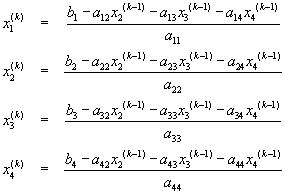
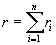 ,
,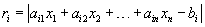 .
.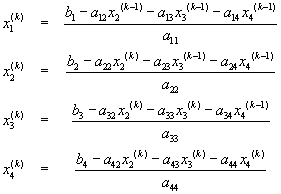
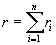 ,
,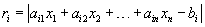 .
.